Abraham Lincoln’s Cyphering Book
by Nerida F. Ellerton and M.A. (Ken) Clements
The oldest extant handwritten manuscript of Abraham Lincoln is his cyphering book, which comprised written solutions to arithmetic problems that he solved when he was at school. The most detailed description and analysis of the manuscript is to be found in chapter 6 of our book, Abraham Lincoln’s Cyphering Book and Ten Other Extraordinary Cyphering Book, published by Springer in 2013. In the text which follows “Abraham Lincoln” will usually be referred to as “AL”.
AL’s cyphering book was, indeed, extraordinary. In the 1820s, relatively few school children in midwestern states such as Illinois, Indiana, Kentucky, Missouri, and Tennessee prepared cyphering books. We currently own about 500 cyphering books prepared by North American school children during the period 1667–1861, but only 11 of those were prepared in the 5 midwestern states—the midwest was a frontier in the early 1800s, paper was scarce, and expensive, and schools were often several miles from the pupils’ homes. Teachers capable of helping children to learn to cypher were hard to find, and arithmetic textbooks were expensive and usually hard to come by. It was one thing for a student in Boston, or New York, or Philadelphia to prepare a cyphering book, but another for a student in the frontier regions to prepare one.
As far as we know, only 22 pages (11 leaves) survive from AL’s cyphering book. Two leaves are held privately, and the others are at the Abraham Lincoln Presidential Library and Museum (Springfield, Illinois), Brown University, Chicago History Museum, Columbia University, Harvard University, Indiana Historical Society, Indiana University, the Library of Congress, the University of Chicago, and Yale University. This unusual scattering of the pages of a manuscript is a direct result of the original cyphering book having been separated into individual leaves by Lincoln’s former law partner, William Herndon, who, following Lincoln’s assassination in 1865, was given the manuscript by Lincoln’s step-mother, Sarah Bush Johnson Lincoln. Herndon sometimes rewarded an “informant” (a person who provided him with information about aspects of Lincoln’s life) with a leaf from the cyphering book. Ultimately, it was only individual leaves which remained, and these became scattered across the nation.
What AL wrote in his cyphering book was not entirely consistent with statements he would later make about what he did at school. In an autobiographical statement written in 1859, AL stated that he cyphered to the “rule of three,” but analysis of the 22 pages shows that, in fact, he cyphered beyond the rule of three. Although Dennis Hanks, who lived with the Lincoln family for much of their Indiana years, told Herndon that AL did not cypher to the double rule of three, on both sides of the leaf now held at Harvard University AL was specifically concerned with the double rule. It is likely that when writing his 1859 autobiographical statement the future President deliberately wanted to give an impression that he was an “intelligent, ordinary man” who had had only a very limited education.
Our analysis of the 22 extant pages indicated that each page of AL’s cyphering book testifies to the future President’s determination to understand what he was writing about. AL did not copy solutions from textbooks or from other cyphering books. That observation fits with the evidence of Lincoln’s stepmother, of Dennis Hanks, and of many of those who went to school with Lincoln, that he was always readin’, writin’ and cypherin’. It is almost certain that most of the entries in his cyphering book were made at school, where there were flat surfaces on which he could write. At home, he was known to have worked out his arithmetic on wooden surfaces (such as walls, and the backs of shovels), and only when at school did he enter solutions to problems in his cyphering book.
Those of AL’s classmates who gave evidence to William Herndon were unanimous in their view that AL was easily the most academically capable of the students at the schools he attended, and they all noted his dedication to cyphering.
AL’s cyphering book was prepared over at least three years—in fact, we, believe it was probably prepared over a period of six or seven years. The first two pages are concerned with simple subtraction, and the handwriting is less mature than on later pages. We would conjecture that the first two pages were prepared in 1819 or 1820, at Andrew Crawford’s school. Some of the later pages were dated 1824, and 1826, by Lincoln.
AL attended school in winter months only, and it is impressive that, somehow, he kept the pages of his cyphering book together over a period of years, so that he might continue to cypher in it when he next returned to school. When, on March 1, 1826, he was writing on the last page of his manuscript, he was moved to write “no room.” He was 17 years of age and had run out of pages, space, and time for cyphering. It was now time for him to move on to the next phase of his life.
Our recent research on AL’s cyphering book has indicated that the order in which the pages were prepared by Lincoln was consistent with a centuries-old abbaco tradition for school arithmetic. That tradition originated in India and in Arab-speaking nations, was taken up by Western European nations around 1200 CE, and was translated to North America in the seventeenth century. The cyphering era closed in the United States in the 1860s.
We now clarify several issues relating to the cyphering tradition, especially as that tradition relates to AL’s cyphering book.
What is a Cyphering Book?
A cyphering book is a handwritten manuscript, probably prepared before 1860, which focused on mathematical content and had the following four properties:
- It was written either by a student (usually a boy, who was at least 10 years old), or by a teacher who wished to use it as a model which could be followed by students preparing their own cyphering books.
- Usually, all entries appeared in ink—as handwritten notes, or problem solutions, or as illustrations. Headings and sub-headings were often presented in decorative, calligraphic style, and occasionally, water-color illustrations were prepared.
- It was dedicated to setting out rules, cases, model examples and exercises associated with a sequence of mathematical topics. Although most cyphering books were specifically concerned with arithmetic, especially commercial arithmetic, some were dedicated to algebra, or geometry, or trigonometry, or to mathematics associated with mensuration, navigation, surveying, fortification, etc.
- The topics covered were sequenced so that they became progressively more difficult. Typically, the first few topics were numeration, the four operations of arithmetic and their applications (especially with regard to money, and measurement), reduction, and the so-called “single rule of three” (often referred to as the “golden rule”). For those few students who went further than this, there were more advanced topics—such as the double rule of three, simple and compound interest, loss and gain, discount, tare and tret, equation of payments, alligation, fellowship, arithmetic and geometric progressions, and mensuration.
What is the Rule of Three?
What is “the rule of three,” which Lincoln specifically mentioned in his 1859 biographical statement? The single rule of three, which summarized the arithmetic of direct proportion, was hugely important for commercial transactions of the 17th, 18th and 19th centuries. But what did it assert, and why was it so important?
Probably the best way to answer that question is to discuss an example from Abraham Lincoln’s cyphering book. One of the pages (which was headed “The Single Rule of Three”) showed Lincoln’s solution to the problem: “If 1 lb sugar cost 4½ what cost 48 lb?” It can be presumed that the unit “pence” should have been given after the 4½.
In textbooks of the time, a solution to this problem would have begun with the following summary statement:
- Pence lb. Pence
1 : 4½ :: 48 : ?
With this special notation, the 1, 4½, and 48 were regarded as the first, second and third terms, respectively, and the rule for obtaining the fourth term was “multiply second by third and divide by first.” Thus, the answer (in pence) to the given “sugar” problem would be found by multiplying 4½ by 48, and then dividing by 1.
For students who did not feel the need to understand what they were doing, the rule merely described what could be done in order to get a correct answer. For them, the “reason for the rule” was unimportant.
But AL always wanted to understand not only what he was doing, but also why he was doing it. His solution to the problem is shown in Figure 1.
The first step should have been to multiply 4½ by 48, but that was far more difficult for AL to do than might have been expected—because by tradition, learning to multiply common fractions and decimals came well after the rule of three in the abbaco sequence. In other, words, AL would not have known how to multiply 4½ by 48 because he had never learned how to multiply fractions. However, he avoided the fractions difficulty by adopting a standard procedure. He converted the 4½ pence to 18 farthings (since there were 4 farthings in a penny, 4½ pence equaled 16 farthings plus 2 more farthings); he then applied the rule-of-three method to get 864 (farthings). He then divided this by 4 to get 216 (pence), and divided that by 12 to get 18 (shillings). This can be seen in Figure 1.

Figure 1: Abraham Lincoln uses the rule of three (c. 1824)
The year when Abraham did this was probably 1824 or 1825. U.S. coins for decimal currency were first minted in the early 1790s, so one might ask why AL was solving problems which used the old English currency of pounds, shillings, pence, and farthings? The short answer to that question is that the old English currency was still legal tender is all parts of the United States—though, in fact, pounds, shillings, pence and farthings had different values in different states!
The rule of three dominated school arithmetic for centuries, but by about 1850 it was becoming less popular. After all, “if 1 lb of sugar cost 4½ pence then, surely, 48 lbs would cost 48 times 4½ pence. One did not need to think in terms of “multiplying second by third and dividing by first.”
Slowly, but surely, educators began to insist that students thought about meanings and their implications, rather than simply applying a rule which they had been told was true. After AL had solved problems using the rule of three he proceeded to tackle problems which required the use of the “double rule of three.” Sometimes this was called the “rule of 5” Because there were 5 known terms (and a sixth had to be determined).
The first problem of this type that he solved in his cyphering book was: “If 100£ in 12 months gain 7£ interest what principal will gain 3£-18S-9d in 9 months?” Such problems also had a special rule which could be applied. Abraham’s solution to the problem is shown in Figure 2. The modern reader would have great difficulty following what AL did, but the future President knew what he was doing and arrived at the correct answer (75 pounds).
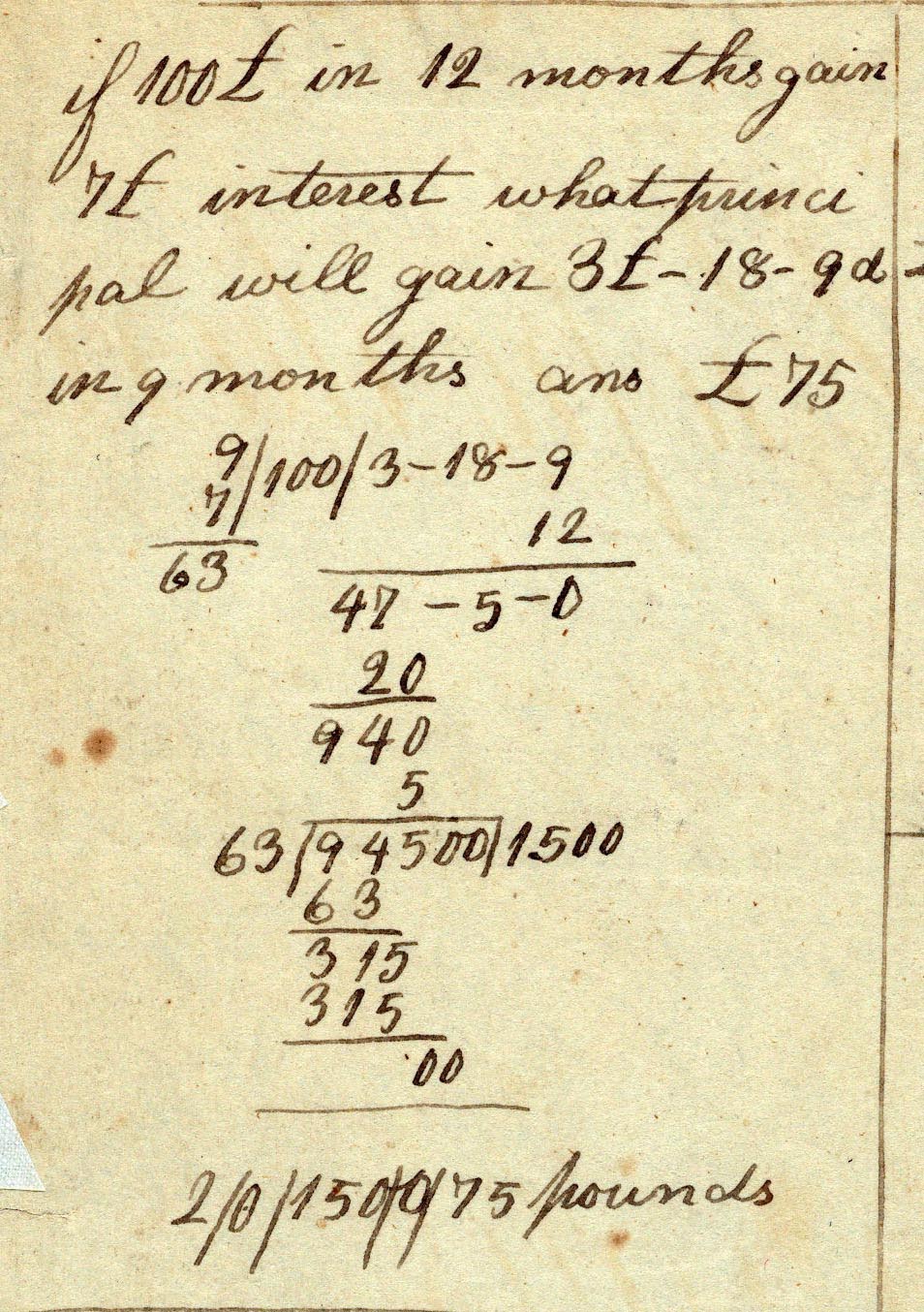
Figure 2; Abraham Lincoln applies the double rule of three
Following his excursion into the double rule of three, Abraham then tackled problems involving simple interest, compound interest, and discount. These later topics required him to go a fair way beyond the single rule of three—something which, 35 years later Abraham did not acknowledge (when he claimed that at school he cyphered to the rule of three).
Casting-Out-Nines in the Lincoln Cyphering Book
Some writers who have examined AL’s cyphering book have commented that he made numerous errors, especially in relation to what was known as “casting-out-nines.” On checking the manuscript, we found that Abraham made very few errors overall. The casting-out-nines technique appeared 18 times altogether—but, in fact all 18 occurrences can be found on just 4 pages, all of which were dedicated to multiplication or division.
Casting-out-nines was a check that was often used, especially with multiplication or division, as a safeguard against making calculation slips. We explain the method by showing how Abraham used it to find the product of 34567834 and 23423.
In order to begin the check, one needed to add the digits for each of the two numbers, and then get the remainders after dividing the sum of the digits for each of the two numbers by 9.
Thus:
3+4+5+6+7+8+3+4 = 40
and, on dividing that sum by 9, one gets 4 and 4 remainder. It is the remainder, 4, which is important for the check. Then, for the second number:
2+3+4+2+3 = 14
Dividing this by 9 gives 1 and 5 remainder—again, it is the 5 which is important for the check. The next step is to multiply the two remainders:
4 × 5 = 20
and if this divided by 9 one gets 2 and 2 remainder. This third remainder should equal the remainder after the sum of the digits in the answer to the original multiplication is divided by 9.
That answer was
809682375782
and the sum of the digits is 65. When 65 is divided by 9 one gets 7 and 2 remainder—and that remainder is equal to the remainder obtained earlier. Hence, it would be concluded that no error had been made in the calculations. AL’s calculations are shown in Figure 3, in which his casting-out-nines check is shown within a small circle, slightly to the left of his calculations.
The casting-out-nines check was not infallible. Sometimes it could suggest an answer was correct when, in fact, it was not. A more reliable check was to divide the answer to the multiplication task by one of the original numbers. Abraham did that (see Figure 3). The result of such a division should be the other original number.
Of the 18 casting-out-nines checks in Abraham’s cyphering book, 17 were correct, and 1 was not. The incorrect check is shown in Figure 4, and the writing was almost certainly done by someone other than AL. The error was to include two 9s in the check—the 9s should have been zeros. So, our conclusion is that in his cyphering book, AL himself carried out 17 casting-out-nines checks, and got all of them correct. Someone else—hopefully not a teacher—did one check, and got it wrong. Furthermore, whoever made that error also seemed to believe that the product of 30000 and 3000 was 90000 (see Figure 4).
On the second page of his cyphering AL penned his famous ditty, “Abraham Lincoln, his hand and pen, he will be good, but God knows when.” This was followed by an excerpt from a hymn by Isaac Watts. It is unlikely that the Watts inclusion was written at the time when the arithmetic on the page was written. The handwriting is much more mature than other writing on the first and second pages. It is likely that at some later period AL was looking for space to write the excerpt from Watts, and he then decided to use vacant space in his cyphering book.

Figure 3: Abraham Lincoln “casts out nines.”

Figure 4: Who made the error in this casting-out-nines check in Abraham Lincoln’s cyphering book?
Most of the extant pages of the cyphering book were probably prepared during the 1824–1825 and 1825–1826 winters, when AL was attending Azel Dorsey’s subscription school.
It is received tradition that during his school days AL had five teachers—in Kentucky there were Zachariah Riney and Caleb Hazel, and in Indiana, Andrew Crawford, James Sweeney, and Azel Dorsey. These individuals ran subscription schools—Abraham probably attended Crawford’s school in the winter of 1819–1820, Sweeney’s school in the winter of 1821–1822, and Dorsey’s school during the winters of 1824–1825 and 1825– 1826. In our research, however, we found reference to a fourth Indiana teacher, James Davis Bryant (or Briant). According to Goodspeed Brothers and Company (1885), Bryant “taught all through this portion of the county, and Abe Lincoln was one of his pupils” (p. 412). Bryant was born in 1800, probably in Kentucky. It appears to have been the case that he was an itinerant teacher who taught in several schools in Spencer County in the early 1820s.
The fact that very few Lincoln biographers and story tellers have referred to James Bryant as one of AL’s teachers begs comment. In and around the Pigeon Creek and Rockport, region Azel Dorsey was highly regarded both as a teacher and a prominent citizen in the community. As his popularity within the local community grew, he took on wider official duties and the demands on his time became greater. We conjecture that Dorsey asked Bryant to take on some of his teaching responsibilities, while he (Dorsey) attended to other matters in town. The possible presence of a fourth Indiana teacher for AL would go some of the way toward explaining the appearance, in AL’s cyphering book, of problems from American arithmetic textbooks by Stephen Pike and Zachariah Jess and, on the final two pages, of problems from the British arithmetic textbook by Francis Walkingame.
According to several of William Herndon’s informants, AL cyphered with all of his Indiana teachers, but the 22 extant pages are all that remain, and most of them were prepared during the last two winters that AL attended school. We conjecture that during those winters Bryant allowed AL to copy from textbooks by Pike, Jess, and Walkingame which Bryant owned—or, alternatively, to copy from a cyphering book that Bryant himself owned which included questions from those three authors.
Did Abraham Consult an Arithmetic by Nicolas Pike or by Stephen Pike?
Several of Herndon’s informants who went to school with Abraham mentioned that he referred to “Pike’s arithmetic,” but it is not clear whether that arithmetic was written by Nicolas Pike (probably in the 1790s) or by Stephen Pike (written at some time between 1810 and 1824). Arguments could be presented for either possibility, or even for the possibility that AL had the book by Nicolas Pike at home, and the teacher (perhaps Bryant) had the text by Stephen Pike at school. Many of the problems which AL solved could be found in editions of Stephen Pike’s book, but several of Herndon’s informants mentioned that AL had an old arithmetic at home. There is not enough evidence to make a strong conclusion on the issue.
Conditions in the Schools Where Abraham Prepared his Cyphering Book
During the winter of 1824–1825 the constant shrill of young voices coming from the 15-or-so children who attended Azel Dorsey’s subscription school house, which was located about two miles from 15-year-old AL’s home in Pigeon Creek, in rural Indiana, would not have surprised any of the locals. Dorsey’s school was a “blab-school” and, as such, students were expected to talk aloud, mainly to themselves, for most of the school day.
Although we cannot provide many specific details about Dorsey’s school, such schools were usually of the log-cabin variety, having just one room, dirt floors, and, of course, no interior bathroom facilities. Inside, there was a large, crudely-constructed fireplace, and rows of split logs provided seating for the students. At the front, there was a teacher’s table, and chair, and along one of the walls was a long, rectangular opening—sometimes covered with greased paper—which, together with candles, was a major source of light in the dim, wintery weather which prevailed. Beneath the rectangular “window” was a flat, slightly sloping bench which was used by those who needed to write in their books. There was only one teacher, and the children were of all ages and sizes—from small 3-, 4-, or 5- year olds to mature young women and farm boys. In non-winter months most of the older boys were expected to work in the fields. There were no blackboards, no slates, hardly any textbooks, limited supplies of rag paper, and home-made ink and quill pens.
For most of a school day students were expected to blab continuously. When a student was called to the teacher’s desk for individual recitation, the other students kept on blabbing. Blab schools were common in the remote regions of Kentucky and Indiana—indeed, almost all schools which young Abraham attended, were of the blab variety.
It is likely that most of the entries in AL’s cyphering book were made during school hours, because the wood-slab table located immediately below the rectangular “window” was the best place to write in order to achieve the desired outcome of neat penmanship and calligraphic headings.
According to Ida Tarbell, Thomas Lincoln did not like Abraham reading or studying much in their home, but his step-mother succeeded in getting Thomas to allow AL to spend time at home on his school work. At school, AL’s writing instrument was a turkey-buzzard quill pen used with home-made brier-root ink.
The cyphering tradition demanded that all entries into a cyphering book should be correct, and therefore AL had to work out solutions to problems before having them checked by the teacher and before writing them in his book. Abraham was well-known for having a strong memory, and it is likely that once he was happy with a solution to a problem he would commit it to memory and then, after having explained it to the teacher during a recitation session, would enter it into his precious cyphering book.
Abraham Lincoln’s cyphering book pages are the earliest known handwritten manuscripts penned by the 16th President. Through these pages we are given a glimpse of the character and skills of a young lad, growing up in Indiana, and destined to change the face of the world. We feel privileged to have held and examined most of these extant pages. His cyphering book represents the start of a lasting legacy that set him on track toward an understanding of the power of numbers well beyond the rule of three. Indeed, we sense that through this beginning, he became intrigued and captivated by the logic and beauty of mathematics.
Nerida F. Ellerton and M.A. (Ken) Clements are on the faculty of Illinois State University. This research was published in “Abraham Lincoln’s Cyphering Book and 10 Other Extraordinary Cyphering Books” (2014).
